Chansh

本文为Neural Networks and Deep Learning一书的学习笔记，仅记录书中的理论部分，省略了实验和例子，文中没有标注的图片都来自于书中。 这本书很适合初学者读，作者写得非常详细，简单易懂，里面涉及到的内容都有解释，还有配有代码和例子，强烈推荐！

一、深度网络架构

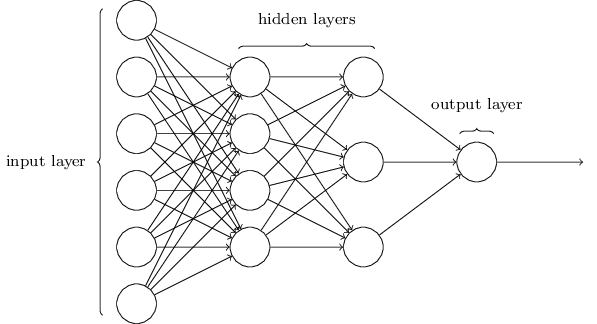第一层和最后一层分别代表输入层和输出层，中间的都叫隐层。一般来说只有前后两层中间有连线，不过也有一些网络是跨层或者同层间相连的。因为是入门，所以这里只讨论最基础的结构。

神经网络每一个节点（神经元）都是前一层多个节点的output的加权和，通过激化函数（Activation）得到的结果。

\begin{eqnarray} z^l&=&w^l a^{l-1}+b^l,
a^l&=&\sigma(z^l). \end{eqnarray}

$a^l$是l层中所有节点的输出值的向量，$w^l$是l-1层中各个节点到l层中各个节点的权值的向量，$b_j^l$是l层各个节点计算时的偏量的向量。函数$\sigma$是激活函数，经常使用的有sigmoid、tanh、softmax、ReLu等。

加权和$z^l$是一种简单的综合前一层中不同节点结果的方法。在加权和外面再套一层非线性的激活函数$\sigma$， 赋予了一个神经元表达更复杂的结果的可能。

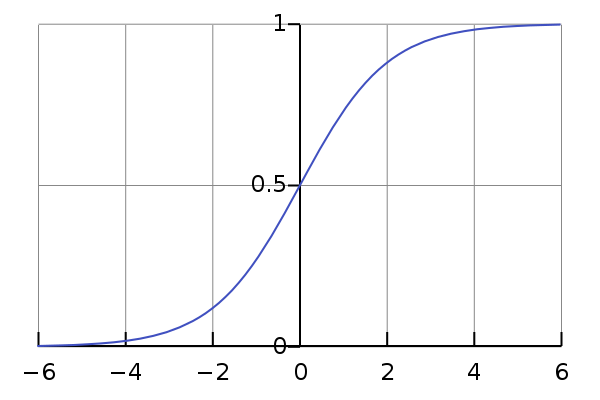
比如使用sigmoid函数，它会将任何输入平滑地映射为一个0到1的值。

$$\sigma(z)=\frac{1}{1+e^{-z}}$$

¹

二、梯度下降（Gradient Descent）

在定义好整个网络的结构之后，我们希望通过训练，得到预测效果最好的参数的值。为了衡量“预测效果”，需要定义一个目标函数（Cost Function），例如：

$$C=\frac{1}{2n}\sum_x\parallel y(x)-a^L(x)\parallel^2$$

$y(x)$是样本的label，$a^L(x)$是输出层输出的结果。$C$越小，则训练效果越好。

然而直接通过数学方法求出最佳参数的表达式非常复杂，而在网络结构比较复杂的情况下根本无法表达和计算。所以，一般采用一种简单的近似方法——梯度下降。

梯度下降的核心思想是，对每个参数求偏导，让参数朝着让$C$变小的方向去改变。反复迭代，直到$C$达到极小值。

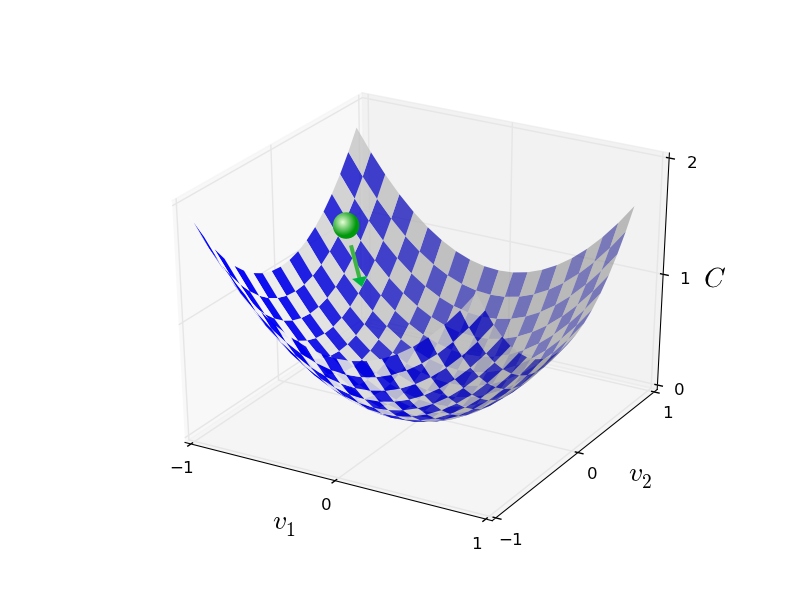
用数学公式表示，$v$为所有参数的向量，记$\nabla C=(\frac{\partial C}{\partial v_1},...,\frac{\partial C}{\partial v_m})$，参数的更新方法为：

$$v \to v' = v-\eta \nabla C,$$

$\eta$是下降的步长。记

$$C_x = \frac{\parallel y(x)-a^L(x) \parallel^2}{2}, \\ C=\frac{\sum C_x}{n},$$

那么$\nabla C=\frac{1}{n}\sum\nabla C_x$。

由于每更新一次参数，都要把整个train data数据集全部跑一遍，太慢。因此，有一种近似的计算方法，随机梯度下降法（Stochastic Gradient Descent），取每m个训练数据为一个mini-batch，设

$$\nabla C=\frac{1}{n}\sum\nabla C_x \approx \frac{1}{m}\sum_{j=1}^{m}\nabla C_{x_j},$$

然后根据每一个mini-batch的计算结果对参数进行一次更新。对整个train data的一次遍历称为一个epoch。由此得到，

$$w_k \to w_k' = w_k-\frac{\eta}{m}\sum_j \frac{\partial C_{x_j}}{\partial w_k}, \\ b_l \to b_l' = b_k-\frac{\eta}{m}\sum_j \frac{\partial C_{x_j}}{\partial b_l}.$$

梯度下降有达到局部最优解的可能，但是可以通过参数的初始化等方法来尽量减小这种可能。从以往经验来说，通常能得到很好的效果。

Written with StackEdit.